5 Analyse : l’ANOVA

5.1 Plus de deux groupes…?

Dans le chapitre précédent, on a analysé les notes de deux groupes d’apprenants (Montréal et Québec). C’est une situation typique pour l’utilisation d’un test \(t\). Si, par contre, on avait trois groupes, on aurait des problèmes, vu que cette méthode est utilisée juste pour un ou deux groupes. Une solution possible serait d’exécuter deux tests \(t\). On verra bientôt que cette approche est très problématique. La solution traditionnelle est donc d’utiliser une autre méthode d’analyse : l’ANOVA. Avant de discuter cette méthode célèbre, il faut bien comprendre pourquoi on évite l’utilisation de plusieurs tests \(t\), ce qui exige l’introduction de deux types d’erreurs en statistique.

5.1.1 Erreur de type I

Une erreur de type I, souvent appelée « faux positif », se produit lorsque nous rejetons à tort une hypothèse nulle qui est en réalité vraie. Dans le contexte de la recherche, cela peut avoir des conséquences importantes, car cela peut mener à des conclusions incorrectes sur l’effet d’un traitement, par exemple, en affirmant qu’un médicament est efficace alors qu’il ne l’est pas. Dans notre contexte, le traitement est la ville où les apprenants étudient le français. Si on arrive à une valeur \(p\) de 0,01, par exemple, on rejette l’hypothèse nulle, c’est-à-dire qu’on conclut que les notes des apprenants des deux villes sont différentes. Toutefois, cette conclusion peut être trompeuse : si, en réalité, au niveau de la population de tous les apprenants de français entre les deux villes, la différence n’existe pas, notre résultat est incorrect. Le problème, naturellement, est qu’on ne sait jamais quelle est la réalité : voilà pourquoi on utilise la statistique.

5.1.2 Erreur de type II

Une erreur de type II décrit la situation contraire à celle d’une erreur de type I : ici, on ne rejette pas l’hypothèse nulle quand, en réalité, elle est fausse. Par exemple, imaginez qu’au niveau de la population, les apprenants à Montréal et à Québec ont des notes vraiment différentes. Cependant, dans notre analyse, notre valeur p est de 0,08. Vu qu’on utilise le seuil de 0,05 (notre valeur alpha : \(\alpha = 0.05\)), on n’est pas capable de rejeter l’hypothèse nulle ici. Cela constituerait une erreur.

5.1.3 Un exercice d’équilibre

Une analyse statistique est donc un exercice d’équilibre : on veut réduire la probabilité des erreurs de type I et II. Bien que les deux soient importants, on a tendance à éviter davantage les erreurs de type I. Voilà pourquoi on n’utilise pas plusieurs tests t dans notre analyse : étant donné notre \(\alpha\), chaque test a une probabilité de 5 % de produire une erreur de type I. Dans un exemple avec trois villes, on aurait besoin d’exécuter deux tests \(t\). En utilisant la formule ci-dessous, on arrive à une probabilité de presque 10 %, ce qui est trop élevé : \(P(erreur) = 1 - (0.95)^2 = 0.0975\). Si on avait quatre villes (c’est-à-dire quatre groupes), on aurait besoin d’exécuter 6 tests \(t\) : \(\frac{n(n-1)}{2}\). Donc, la probabilité d’une erreur de type I serait de \(P(erreur) = 1 - (0.95)^6 \approx 0.735\) (!). On voit donc que l’application de plusieurs tests devient rapidement problématique.

\[P(\text{Erreur de type I}) = 1 - (1 - \alpha)^n\]

Votre tour

Chargez le fichier villes2.csv. Essayez d’exécuter un test \(t\) sur note en fonction de ville. Avez-vous réussi? Comment pourriez-vous utiliser des tests \(t\) pour analyser ces données? Vous aurez besoin des fonctions pratiquées dans le chapitre 2.

5.2 Introduction à l’ANOVA

L’Analyse de la Variance, ou ANOVA, est une méthode statistique utilisée pour comparer les moyennes de plusieurs groupes (typiquement, > 2 groupes). L’idée principale de l’ANOVA est d’examiner si les différences observées entre les moyennes des groupes sont suffisamment grandes pour qu’on puisse conclure qu’elles ne sont pas dues au hasard, mais plutôt à un effet réel. Autrement dit, la différence entre les groupes analysés est-elle statistiquement réelle? Par exemple, si vous testez, à partir d’un examen de grammaire, l’effet de trois villes canadiennes sur l’acquisition du français langue seconde, l’ANOVA peut vous aider à déterminer si les différences dans les notes de l’examen entre les groupes sont significatives. Imaginons trois groupes d’apprenants de français qui viennent au Canada pour étudier la langue pendant six mois. Un groupe s’installe à Montréal, un autre groupe s’installe à Québec, et le troisième groupe décide d’aller à Calgary. À la fin de la période en question, on teste la compétence grammaticale des apprenants à partir de l’examen mentionné ci-dessus. Comment savoir si les différences dans les notes sont vraiment réelles (et pas dues au hasard)? Le problème, naturellement, est que la variation est toujours présente dans les données. Par conséquent, il est naturel que les groupes n’aient pas exactement la même note moyenne.

Pour comprendre l’ANOVA, il est utile de penser à deux sources principales de variabilité dans les données : la variabilité entre les groupes (due à des différences réelles entre les groupes) et la variabilité à l’intérieur des groupes (due à des variations naturelles ou aléatoires parmi les individus d’un même groupe). L’ANOVA compare ces deux sources de variabilité pour évaluer si les différences entre les groupes sont suffisamment grandes par rapport à la variabilité naturelle pour être significatives.

Mathématiquement, l’ANOVA repose sur une équation clé :

\[ F = \frac{\text{Variabilité entre les groupes}}{\text{Variabilité à l'intérieur des groupes}} \]

Le F est une mesure du rapport entre ces deux sources de variabilité. Si ce rapport est élevé, cela signifie que la variabilité entre les groupes est grande par rapport à la variabilité interne, ce qui suggère qu’il pourrait y avoir un effet réel. Pour déterminer si ce ratio est suffisamment grand, on le compare à une valeur critique issue d’une distribution appelée distribution F.

5.3 Le calcul : trois villes

Dans le fichier villes2.csv, on a une version élargie de villes.csv : maintenant, notre étude considère trois villes où des apprenants étudient le français. La troisième ville est la ville de Calgary. Avant de commencer notre discussion, il est important de se rappeler quelle est l’hypothèse nulle.

L’hypothèse nulle

\[H_0 = \mu_{Calgary} = \mu_{Montréal} = \mu_{Québec}\]

Les moyennes des notes des trois villes sont identiques. Autrement dit, il n’y pas de différences entre les moyennes des villes.

On ne calcule jamais une ANOVA de façon manuelle. Ce n’est pas difficile, mais c’est fastidieux. Toutefois, il est très utile de le faire au moins une fois pour mieux comprendre le processus. Vous savez déjà qu’une ANOVA est effectivement une analyse de variance. La variance totale dans les données peut être décomposée en la variance expliquée par les variables examinées (ici, juste ville), c’est-à-dire le numérateur dans la fraction ci-dessus, et la variance qui n’est pas expliquée (résiduelle), c’est-à-dire le dénominateur de la fraction ci-dessus. La variance ici est calculée à partir de la somme des carrés des écarts, ou SCE. Il faudra donc calculer :

Le calcul de la valeur F

Variation entre les groupes : \(SCE_{\text{entre}} = \sum_{j=1}^{k} n_j (\bar{x}_j - \bar{X}_{\text{total}})^2\)
Variation à l’intérieur des groupes : \(SCE_{\text{intra}} = \sum_{j=1}^{k} \sum_{i=1}^{n_i} (x_{ij} - \bar{X}_j)^2\)
Dégrés de liberté entre : \(k - 1\)
Dégrés de liberté intra : \(N - k\)
Valeur F :

\[F = \frac{\frac{SCE_{\text{entre}}}{ddl_{entre}}}{\frac{SCE_{\text{intra}}}{ddl_{intra}}}\]

Signification des symboles

\(k\) : nombre total de groupes (3 villes)
\(n_j\) : nombre d’observations dans le groupe \(j\) (50 obs par ville)
\(x_{ij}\) : valeur de l’observation \(i\) dans le groupe \(j\)
\(\bar{x}_j\) : moyenne des observations pour le groupe \(j\)
\(\bar{X}_{\text{total}}\) : moyenne globale de toutes les observations
\(SCE_{\text{entre}}\) : somme des carrés expliquée par la variation entre les groupes
\(SCE_{\text{intra}}\) : somme des carrés expliquée par la variation à l’intérieur des groupes
\(ddl_{\text{entre}}\) : degrés de liberté entre les groupes (\(k - 1\))
\(ddl_{\text{intra}}\) : degrés de liberté à l’intérieur des groupes (\(N - k\), où \(N\) est le nombre total d’observations)
\(F\) : valeur du test \(F\), qui compare la variance entre les groupes à la variance à l’intérieur des groupes

5.3.1 Le SCE entre

On profite du calcul manuel pour réviser quelques fonctions de dplyr déjà explorées dans le chapitre d’introduction à R (ainsi que dans Barnier (2023)). Dans le code ci-dessous, on charge l’extension et les données. Ensuite, on créé des variables importantes pour le calcul manuel de la valeur F pour l’ANOVA.

library(tidyverse)
villes = read_csv("donnees/villes2.csv")

# Nombre d'observations :
N = nrow(villes) # = le nombre de lignes dans le tableau

# Moyenne totalle X :
X = mean(villes$note)

# Nombre de groupes k :
k = 3 # trois villes

Notre prochaine étape consiste à calculer les sommes des carrés écarts (SCE). On commence par la simplification de notre tableau : vu qu’on n’utilisera pas la colonne duree, on l’enlève avec la fonction select(). Après, on crée un nouveau tableau, entreVilles, qui contiendra les colonnes essentielles pour notre calcul. Le code entre les lignes 7 et 13 nous donne un tableau avec toutes les variables nécessaires : la note moyenne (moyenne) et la quantité d’observations pour chaque ville (n), ainsi que la différence entre la moyenne de chaque ville et la moyenne générale des trois villes (X, créé ci-dessus). Finalement, on élève cette différence au carré (CE) et on multiplie CE par n, ce qui nous donne la colonne finale n_CE. Notre tableau est imprimé entre les lignes 17 et 21, donc observez attentivement les valeurs. Veuillez noter que la fonction n() dans la ligne 9 nous donne le nombre d’observation selon le groupement par ville (.by = ville), ce qui est très pratique.

Lorsqu’on a calculé toutes ces variables, il faut juste sommer les trois valeurs dans la colonne n_CE et diviser le résultat par k-1. Cela nous donne notre SCE entre groupes, représenté par la variable SCEentre dans la ligne 27, dont la valeur est imprimée dans la ligne 28. Finalement, on utilise la fonction pull() ici pour extraire des valeurs d’un tableau (d’un tibble dans notre cas).

# Ajoutons la moyenne de chaque ville au tableau :
villes = villes |> 
  select(-duree) |> 
  mutate(moyenne = mean(note), .by = ville)

# Un tableau simples avec la moyenne de chaque ville
entreVilles = villes |> 
  summarize(moyenne = mean(note), 
            n = n(),
            .by = ville) |> 
  mutate(diff = moyenne - X,
         CE = diff^2,
         n_CE = n * CE)

entreVilles
#> # A tibble: 3 × 6
#>   ville    moyenne     n   diff     CE  n_CE
#>   <chr>      <dbl> <int>  <dbl>  <dbl> <dbl>
#> 1 Calgary     67.0    50 -3.25  10.5   527. 
#> 2 Montréal    69.6    50 -0.671  0.451  22.5
#> 3 Québec      74.2    50  3.92  15.3   767.

SCEentre = entreVilles |> 
  summarize(SCEentre = sum(n_CE)) |> 
  pull() 

SCEentre
#> [1] 1316.82

# La moyenne des la SCEentre :
MSCEentre = SCEentre / (k - 1)
MSCEentre
#> [1] 658.4101

Avant de continuer, assurez-vous que la relation entre l’équation de \(SCE_{entre}\) et son implémentation dans les codes ci-dessus est claire. Remarquez l’utilisation de .by = pour grouper les données dans chaque ville avant de calculer les moyennes et le nombre d’observations, par exemple.

5.3.2 Le SCE intra

Observez le code ci-dessous. C’est un code très économique qui est capable d’accomplir toutes les étapes nécessaires pour calculer la somme des carrés des écarts :

On calcule les écarts. Rappelez-vous qu’on a déjà calculé la moyenne pour chaque ville (colonne moyenne). Donc, pour calculer diff, on n’a pas besoin de grouper les données.
On élève diff au carré
Finalement, on somme les carrés des écarts et on divise le résultat par N - k.

SCEintra = villes |> 
  mutate(diff = note - moyenne) |> 
  mutate(CE = diff^2) |> 
  summarize(SCEintra = sum(CE)) |> 
  pull()

SCEintra
#> [1] 16609.83

# La moyenne des la SCEintra :
MSCEintra = SCEintra / (N - k)
MSCEintra
#> [1] 112.992

5.3.3 La valeur F

Maintenant, on est prêt à calculer notre valeur F à partir des moyennes des SCE calculées. Veuillez noter que MSCEentre équivaut à \(\frac{SCE_{entre}}{ddl_{entre}}\), par exemple. Donc, la ligne 1 ci-dessous nous donne exactement l’équation de la valeur F

valeurF = MSCEentre / MSCEintra

valeurF 
#> [1] 5.82705

On constate que la valeur est supérieure à 1. Cela signifie que la variance entre les groupes est supérieure à la variance dans chaque groupe. Autrement dit, la variable ville semble générer des notes moyennes différentes pour les apprenants. Il faut toutefois vérifier la valeur p pour confirmer ce résultat.

Dans le passé, on consultait un tableau des valeurs pour déterminer la limite F à partir de laquelle on obtient un résultat significatif, en fonction d’une valeur \(\alpha\). Consultez un exemple de tableau ici.¹ L’avantage d’utiliser une fonction comme pf(), montrée ci-dessous, est qu’elle nous permet de calculer une valeur de p exacte.

pf(valeurF, df1 = k-1, df2 = N-k, lower.tail = F)
#> [1] 0.003669896

Voilà! On confirme une valeur p significative. Autrement dit, il n’est pas vrai que les notes moyennes sont identiques à travers les trois villes. Donc, on rejette l’hypothèse nulle. Heureusement, on n’a pas besoin de faire ce calcul de façon manuelle : on utilisera une fonction très pratique pour arriver à nos résultats à partir d’ici.

5.4 L’analyse : trois villes

Voyons comment une fonction en R est capable d’automatizer toutes les étapes décrites ci-dessus. Avant d’utiliser cette fonction, il est utile d’examiner une séquence typique de quatre étapes qui seront utilisées toujours dans notre cours :

Chargez le fichier de données
Vérifiez sa structure
Créez une figure pour visualiser les patrons d’intérêt
Utilisez une méthode statistique pour analyser les patrons en question

On vera comment exécuter une ANOVA dans l’étape 4 ci-dessous. Veuillez noter que les calculs manuels ci-dessus se concentrent sur l’étape 4 aussi, et que même si on décidait de faire les chose à main, il faudrait suivre les autres étapes, naturellement (p. ex., la création des figures).

1. Chargez les données

library(tidyverse)
villes = read_csv("donnees/villes2.csv")

2. Vérifier les premières lignes

villes
#> # A tibble: 150 × 3
#>     note ville   duree
#>    <dbl> <chr>   <dbl>
#>  1  52.5 Calgary    36
#>  2  68.7 Calgary    15
#>  3  48.3 Calgary    18
#>  4  96.9 Calgary    12
#>  5  71.6 Calgary    13
#>  6  48.6 Calgary    34
#>  7  74.7 Calgary    22
#>  8  79.8 Calgary    25
#>  9  76.5 Calgary    29
#> 10  58.9 Calgary    30
#> # ℹ 140 more rows

3. Créez une figure

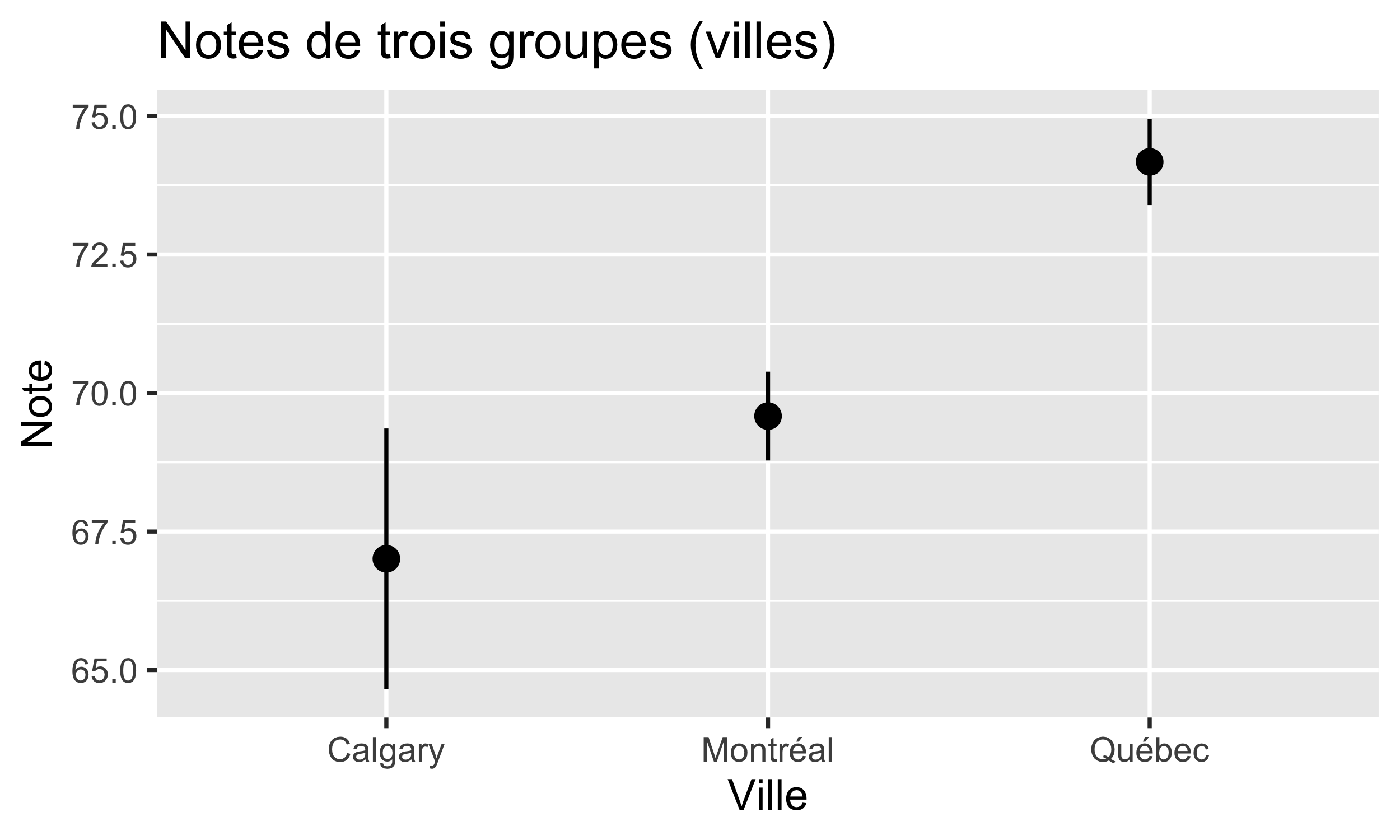
Code

ggplot(data = villes, aes(x = ville, y = note)) + 
  stat_summary() +
  labs(x = "Ville",
       y = "Note",
       title = "Notes de trois groupes (villes)")

Observez la figure. Vous voyez les notes moyennes ainsi que les erreurs standards des moyennes. Considérez chacune des trois comparaisons : Calgary vs Montréal, Calgary vs Québec, et Montréal vs Québec. Quelles différences pensez-vous être statistiquement significatives?

4. Analysez les données : ANOVA

On est maintenant prêt à exécuter notre anova. On utilise la fonction aov() en R. Ensuite, on utilise summary() pour imprimer un résumé du modèle :

notreAnova = aov(note ~ ville, data = villes)
summary(notreAnova)
#>              Df Sum Sq Mean Sq F value  Pr(>F)   
#> ville         2   1317   658.4   5.827 0.00367 **
#> Residuals   147  16610   113.0                   
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Observez l’output de la fonction. Voici chaque élément dans l’output généré par la fonction :

Df : Degrees of freedom. Cette colonne nous donne les dégrés de liberté (ddl) de la variable ville. Il s’agit d’un concept clé en statistique qui désigne le nombre de valeurs indépendantes qui peuvent varier dans une analyse sans violer une contrainte. On a trois villes, donc notre dégré de liberté est 2 (\(n-1\)).
Sum Sq : la variabilité des données. La première ligne nous donne 1317, ce qui représente la variabilité des données explicable à partir de la variable ville. La variabilité des résiduelles (16610) nous montre le complément de la variabilité : c’est la variation qui n’est pas expliquée par ville.
Mean Sq : si on divise Sum Sq par Df, on arrive à la colonne Mean Sq. Cette colonne nous permet de comparer la variabilité expliquée à travers plusieurs source de variation, vu qu’elle normalise la variation par rapport aux dégrés de liberté de chaque variable.
F value : La valeur F nous donne le ratio entre la variation expliquée par ville et la variation dans chaque groupe (c’est-à-dire, la variation qui n’est pas expliqué par ville; les résiduelles). Essentiellement, F = Mean Sq d’une variable divisé par Mean Sq des résiduelles.
Pr(>F) : la valeur p de chaque variable (il y en a juste une dans notre ANOVA)

On conclut donc qu’il faut rejeter l’hypothèse nulle : ce n’est pas vrai qu’il n’y a pas de différence entre les notes moyennes des villes. Voici comment vous pourriez rapporter nos résultats :

Notre ANOVA a confirmé que la ville où les apprenants étudient le français a un effet statistiquement significatif sur leurs notes moyennes : F(2, 147) = 5.827, p = 0.00367.

Remarquez que le modèle utilisé suit la structure suivante :

F(x, y), où
- x = Df de la variable d’intérêt
- y = Df des résiduelles

Si on avait deux variables d’intérêt, on indiquerait deux valeurs : F(x1, y) et F(x2, y).

5.5 D’où vient la différence…?

Une ANOVA nous permet de dire si une différence existe ou non. Autrement dit, elle nous permet de rejeter ou de ne pas rejeter l’hypothèse nulle, soit qu’il n’y a pas de différences entre les moyennes des groupes analysés (les trois villes, dans notre cas). Toutefois, on ne sait pas où sont les différences. Est-ce qu’un résultat significatif vaut dire qu’il y a une différence entre Montréal et Québec? Entre Calgary et Montréal? Entre Calgary et Québec?

Pour répondre à ces questions, il faut complémenter notre ANOVA avec des tests post-hoc, qui nous permettent de vérifier toutes les comparisons possibles. Ce type de test utilise automatiquement une correction pour les valeurs p, etant donné le problèmes des tests multiples discuté plus tôt (Section 5.1.1).

5.5.1 Tukey HSD

L’une des façons de dériver les comparaisons multiples à partir de notre ANOVA est d’utiliser le test Tukey HSD (Honest Significant Difference). C’est une méthode post-hoc utilisée après une ANOVA pour comparer toutes les paires de moyennes entre les groupes. Il permet de déterminer quelles différences spécifiques entre les groupes sont significatives, tout en contrôlant le risque d’erreur de type I (faux positifs). Intuitivement, Tukey ajuste les seuils de significativité pour tenir compte du fait que plusieurs comparaisons sont effectuées en même temps (p. ex., notre discussion plus tôt à propos des multiples tests t). Cela garantit que les conclusions restent fiables, même avec de nombreuses comparaisons. Ce test est particulièrement utile quand l’ANOVA indique une différence globale, mais qu’on souhaite savoir précisément où ces différences se situent.

La fonction tukeyHSD() est très pratique : à partir d’une ANOVA, elle renvoie toutes les comparaisons des villes dans nos données.

TukeyHSD(notreAnova)
#>   Tukey multiple comparisons of means
#>     95% family-wise confidence level
#> 
#> Fit: aov(formula = note ~ ville, data = villes)
#> 
#> $ville
#>                      diff        lwr       upr     p adj
#> Montréal-Calgary 2.574834 -2.4587731  7.608442 0.4484897
#> Québec-Calgary   7.163834  2.1302269 12.197442 0.0027498
#> Québec-Montréal  4.589000 -0.4446075  9.622608 0.0818846

On voit ici qu’il n’y a qu’une comparaison significative : celle entre Québec et Calgary. La colonne p adj nous donne des valeurs p qui sont ajustées par rapport aux comparaisons multiples. Rappelez-vous que notre hypothèse nulle suppose que il n’existe pas de différences entre les trois villes. Donc, maintenant on sait exactement pourquoi notre ANOVA nous a donné une valeur de p significative.

5.6 Synthèse des fonctions

Les deux fonctions les plus importantes du chapitre :

aov(y ~ x, data = ...) pour exécuter une ANOVA
summary() pour imprimer les résultats (fonction générale qui est applicable à plusieurs objets en R)
tukeyHSD() pour générer un test posthoc de comparaisons multiples

Pratique

Bien qu’on n’utilisera pas les ANOVAs directement dans le cours, les concepts discutés ici seront essentiels. Assurez-vous qu’ils soient clairs avant de continuer vers le chapitre sur la régression linéaire (dont l’ANOVA est un cas spécial). Ce pratique-ci vous aidera à réviser attentivement les concepts en question.

Question 1. Créez un sous-ensemble des données à partir de villes2.csv où vous considérez juste les villes de Québec et Montréal. Exécuter un test t pour vérifier la différence entre les deux villes. Qu’est-ce que vous notez dans les résultats? Comparez ces résultats au résultat de notre test posthoc Tukey ci-dessus. Expliquez ce que vous remarquez.

Question 2. Créez un sous-ensemble des données à partir de villes2.csv où vous considérez juste les notes supérieures à 80,0. Calculez une ANOVA manuellement et comparez votre travail aux résultats de la fonction aov(). Générez des comparaisons multiples avec Tukey. Les résultats à partir de ce sous-ensemble sont-ils différents des résultats discutés ci-dessus pour les données complètes?

Cherchez le tableau pour \(\alpha = 0.05\). Dans ce tableau, localisez la colonne df1 = 2 (nos degrés de liberté pour ville) et la ligne \(\infty\) pour df2, car le ddl pour nos observations est élevé (147 = 150 observations - 3 villes). Vous verrez que la valeur dans cette cellule est de 2,99. Comme notre valeur de F est supérieure à cette valeur, cela signifie que notre p est significatif, c’est-à-dire \(p < 0,05\).↩︎